Fourier-Reihen - von Wolfram MathWorld
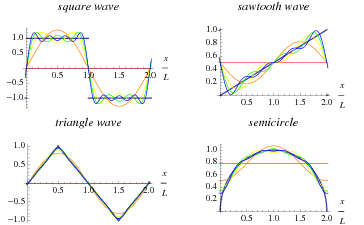
Eine Fourier-Reihe ist eine Erweiterung einer periodischen Funktion in Bezug auf eine unendliche Summe von Sinus- und Kosinusfunktionen. Fourier-Reihe nutzt die Orthogonalitätsbeziehungen der Sinus- und Kosinus-Funktionen. Die Berechnung und Untersuchung der Fourier-Reihe wird als harmonische Analyse bekannt und sind äußerst nützlich als eine Möglichkeit, eine beliebige periodische Funktion in einen Satz von einfachen Mitteln zu brechen, die eingesteckt werden können, einzeln gelöst und rekombiniert dann die Lösung auf dem zu erhalten ursprüngliches Problem oder eine Annäherung an ihn zu, was die Genauigkeit oder praktisch erwünscht ist. Beispiele für sukzessive Approximationen auf allgemeine Funktionen Fourierreihe unter Verwendung sind oben dargestellt.
Insbesondere, da hält das Überlagerungsprinzip für Lösungen einer linearen homogenen gewöhnlichen Differentialgleichung. wenn solche kann eine Gleichung in dem Fall eines einzelnen sinusoid gelöst werden, die Lösung für eine beliebige Funktion steht sofort zur Verfügung, indem die ursprünglichen Funktion als Fourierreihe ausdrückt, und dann in der Lösung für jede sinusförmigen Komponente anschließen. In einigen speziellen Fällen, wo die Fourier-Reihe kann in geschlossener Form summiert wird, kann diese Technik auch analytische Lösungen ergeben.
Jeder Satz von Funktionen, die ein vollständiges orthogonales System bilden, besitzen eine entsprechende verallgemeinerte Fourier-Reihe analog zur Fourier-Reihe. Zum Beispiel gibt mit Orthogonalität der Wurzeln einer Bessel-Funktion der ersten Art eine so genannte Fourier-Bessel-Reihe.
Die Berechnung der (üblichen) Fourier-Reihe basiert auf den integralen Identitäten basierend
Unter Anwendung des Verfahrens für eine verallgemeinerte Fourier-Reihe. die übliche Fourierreihe Sinus- und Kosinusfunktionen beteiligt ist, indem sie und erhalten. Da diese Funktionen ein vollständiges orthogonales System über bilden, wird die Fourier-Reihe einer Funktion gegeben ist durch
und, 2, 3. Man beachte, dass der Koeffizient des konstanten Term ist in einer besonderen Form im Vergleich zu der allgemeinen Form für eine verallgemeinerte Fourier-Reihen zu erhalten, um Symmetrie mit den Definitionen und geschrieben worden.
Eine Fourier-Reihe konvergiert auf die Funktion (gleich die ursprünglichen Funktion an Punkten der Kontinuität oder den Durchschnitt der zwei Grenzen an den Punkten der Unstetigkeit)
wenn die Funktion Dirichlet erfüllt Bedingungen so genannte. Dini-Test gibt eine Bedingung für die Konvergenz der Fourier-Reihe.
Als Ergebnis in der Nähe von Unstetigkeitsstellen, ein „Klingel“, wie das Gibbs-Phänomen bekannt. kann oben dargestellt, auftreten.
Für eine Funktion periodisch auf einem Intervall statt, kann eine einfache Änderung von Variablen verwendet werden, um das Intervall der Integration zur Transformation von zu. Lassen