Die Normalkurve und Galton Verwaltungsrat
Die Normalkurve und Galton Board
von Paul Trow
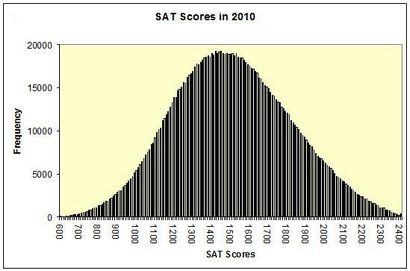
In dem Diagramm ist der Bereich der möglichen Werte auf der horizontalen Achse angezeigt. Für jede Partitur, zeigt die Höhe der vertikalen Balken an diesem Punkt die Anzahl der Schüler, die diese Punktzahl erhalten. Die Spitzen der Stäbe verfolgen eine vertraute Form aus - die normale cuve.
Warum werden in der Normalverteilungskurve so oft bis in vielen scheinbar nicht verwandten Bereichen der Studie? Im neunzehnten Jahrhundert, Sir FrancisGalton, einer der Pioniere der statistischen Theorie, erfand eine mechanische Vorrichtung, die die Normalverteilungskurve zeigt, wie natürlich aus der Kombination einer großen Anzahl von unabhängigen zufälligen Ereignissen oder Faktoren entsteht. Eine Neuschöpfung Galton des Geräts ist unten dargestellt.

Das Gerät besteht aus einem arrayof Stifte auf einer vertikalen Platte montiert. Wenn die Leiterplatte betrieben wird, fällt eine Folge von Kugeln auf die Oberseite des Arrays. Wenn ein Ball einen Stift trifft, prallt er nach links oder rechts mit gleicher Wahrscheinlichkeit und fällt dann auf die nächste Ebene. Wenn der Ball die letzte Stufe erreicht hat, fällt es in einen der Behälter an der Unterseite. Da die Kugeln in die Behälter stapeln, bilden sie eine Form, die eine Normalkurve ähnelt.
Um ein Video von einer kleinen Computersimulation von Galton Brett zu sehen, mit nur 6 Ebenen von Stiften, klicken Sie hier.
Das Bild unten zeigt das letzte Bild der Animation.
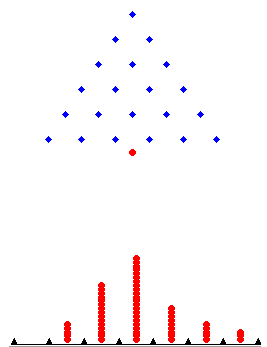
Wie zu erwarten, ist es wahrscheinlicher, dass ein Ball als in einem Behälter in der Nähe von beiden Enden in eines des Behälters in der Mitte landen (0 oder 6). Der Grund dafür ist, dass es mehr Wege eine Kugel als in Behälter in der Nähe der Seiten, dass die Führung in Behälter in der Nähe der Mitte zu nehmen. Um zu sehen, warum sollten Sie das folgende Experiment, das einen zufälligen Pfad für einen Ball simuliert. Werfen Sie eine Münze 6 Mal und notieren Sie die Reihenfolge der Köpfe und Schwänze, die Sie erhalten. Wenn der i-te Münzwurf Köpfe ist, springt der Ball nach rechts auf der Ebene i - wenn der i-ten Wurf Schwänze ist, der Ball nach links springt. wenn die Sequenz der Münzwürfen Zum Beispiel ist H, H, T, H, H, T, nimmt der Ball die pathshown im Diagramm unten.
Beachten Sie, dass die Anzahl der Köpfe in diesem Beispiel 4 ist, und dass der Ball landet in Bin-Nummer 4. Wenn Sie ein paar Beispiele versuchen, können Sie sich selbst davon überzeugen, dass für jede Folge von Münzwürfen, die Zahl des Faches der Ball landet in immer gleich die Anzahl, wie oft die Münze Köpfe kommt. Folglich ist die Anzahl von Pfaden zu bin Nummer 4 ist die Anzahl von Sequenzen von 6 Münzwürfen der genau 4 Köpfe haben. Es stellt sich heraus, dass es 15 solche Sequenzen. (Wenn Sie dies nicht glauben, versuchen, sie aufzuschreiben.)
Auf der anderen Seite gibt es nur einen Pfad tobin 0, zur Sequenz aller tails entspricht, was bedeutet, dass die Kugel auf jeder Ebene nach links springt. Als Ergebnis ist eine Kugel 15 Mal häufiger 0 in Bin 4 als ist landen.
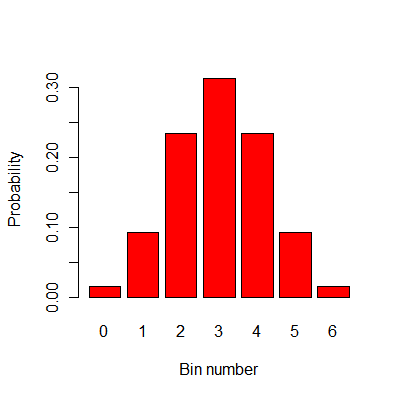
Um die Wahrscheinlichkeit zu finden, die eine Kugel in sind landen i, teilen Sie die Anzahl der Pfade zu bin ich durch die Gesamtzahl der Pfade zu allen bins.The letztererletztereletzteres Zahl ist 2 6 = 64, becausethe Ball in einem von zwei Möglichkeiten, hüpft auf jeder Ebene und sind 6 Ebenen. Die Tabelle unten zeigt die Anzahl von Pfaden zu jedem Behälter, und die Wahrscheinlichkeiten, daß eine Kugel in einem bestimmten Fach landen wird.
Die folgende Abbildung zeigt die grafisch Wahrscheinlichkeiten.
Die Binomialverteilung und die Normalapproximation
Diese Verteilung der Wahrscheinlichkeiten in dem in der Tabelle und Grafik oben gezeigt ist ein Sonderfall der Binomialverteilung. Die allgemeine Binomialverteilung hat zwei Parameter:
- n - die Anzahl der Münzwürfen
- p - die Wahrscheinlichkeit, dass die Münze Köpfe kommen wird jeden beliebigen Wurf.
Die Binomialverteilung gibt die Wahrscheinlichkeit des Erhaltens genau k Köpfe in n Münzwürfen, für jede ganze Zahl k zwischen 0 und n ist. In dem obigen Beispiel n = 6 und die Wahrscheinlichkeit p = 0,5 - mit anderen Worten, die Münze ist fair.
Die obigen Beispiele zeigen, warum die Verteilung der ballsin Galton-Vorstand die Form einer Binomialverteilung hat. Aber whatdoes dies mit der normalen Kurve zu tun? Die Antwort ist, dass für große n, eine binomialen Zufallsvariable, withparameter p = 0,5 ist, hat etwa die gleiche Verteilung wie die normalrandom Variable mit der gleichen „Form“ - das heißt, der gleichen Mittelwert und die Standardabweichung. Dies ist ein Spezialfall eines berühmten Ergebnisses des zentralen Grenzwertsatz genannt.
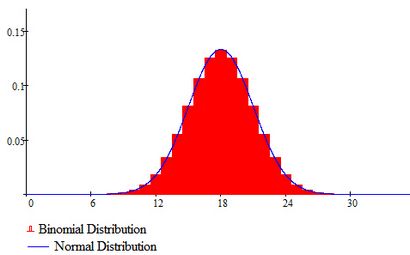
Es stellt sich heraus, dass eine binomische Zufallsvariable mit dem Parameter p = 0,5 N / 2 und der Standardabweichung .Für Beispiel bedeuten hat, wenn n = 36, 18 die mittlere und die Standardabweichung beträgt 3. Das folgende Diagramm zeigt die Binomialverteilung mit diesen Parameter, Together einer Normalkurve mit dem Mittelwert und der Standardabweichung 18 3.
Schließlich ist hier ein Bild von dem aktuellen Board Galton gebaut, die in dem University College in London ist noch vorhanden. Die Kugeln, die durch die Stifte fallen gelassen wurden tatsächlich Bleischrot.
